Hey guys,
Imagine you are starting a new cellphone business, let’s called it BCC - Best Cellphone Company. After years of development, you designed the final product! You created a product that changes the status quo !
Now it is fun time: time to sell it!
How are you going to place your innovative product in the market?
- Are you going to sell it for a low price to get revenue based on quantity?
- Or are you going to start with high price imagining that the product will be recognized, although your new company does not have a established brand?
SOLUTION : Let’s use market data to find the best price for your product!
Key Takeaways:
1. Data Treatment
2. Dealing with Multiple Class problems : One-vs-Rest (OvR) and One-vs-One (OvO)
3. Comparison between Logistic Regression and Support Vector Machine
Source : Kaggle Mobile Prediction Classification
#Importing Libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
#Importing dataframe
test = pd.read_csv('../data/datasets_11167_15520_test.csv')
train = pd.read_csv('../data/datasets_11167_15520_train.csv')
Before we begin,
I would like to share a mindset about working with data that may be silly, but it makes all sense for me.
For any important event - for instance, a job interview - what do you do prior to your arrival? You prepare yourself! You search for information on the internet, social media (Instagram, Facebook, LinkedIn), employees … You do it because you want to create a picture in your mind of the company, its work environment and the position that you are applying for.
Let me tell you: considering data, it is not different at all! You must get to know the data: bring to a dinner and have some great chat at a coffee shop. Then, when you feel prepared, when you feel that you know everything about them, you can ask for a commitment. Then, you start to create a deeper connection by using statistical learning models !
A - Checking out dataframes, description and the goal
Here, I superficially check how the dataset is presented.
-
Total number of Attributes: 21
- Are there discrete variables? - Yes
- Details: blue (Bluetooth - 0 No / 1 Yes), dual_sim (0 No / 1 Yes), four_g (0 No / 1 Yes), three_g (0 No / 1 Yes), touch_screen (0 No / 1 Yes), wifi (0 No / 1 Yes)
- Are there any continuous variables? - Yes
- Details: battery_power,clock_speed,int_memory,n_cores*,m_dep,mobile_wt,pc,px_height,px_width,ram,sc_h,sc_w,talk_time
- Are there discrete variables? - Yes
-
Output variable: price_range
- Discrete variable
- Multiclass - 4 different classes: 0 (low cost), 1 (medium cost), 2 (high cost) and 3 (very high cost)
GOAL: Based on mobile attributes, our goal is to predict the class of our new cellphone’s price.
# Train dataset
train.head()
# Test dataset
#Here, I drop the "id" column that we are not going to need it.
test.drop('id',inplace=True,axis=1)
test.head()
B - Let’s dive in the output variable: price_range
Here, we start BY checking missing values. By its name already says, missing values are data that were not entered and we cannot use them as it is. There are many ways to treat missing data and several articles that show how to deal with it:
- Filling it up with the arithmetic, harmonic mean
- Filling it up with the mode and median
- Or just ignoring and deleting them.
#Let's dive in the output variable
y_train = train.price_range.values
#Count plot
sns.countplot(x='price_range',data=train)
plt.title('Count plot')
#Equal number of values for each class - Great!
#Check missing values
miss = (1-train.price_range.isnull().value_counts()/train.price_range.count())*100
'There is {}% of missing values in the output variable'.format(miss[0])
'There is 0.0% of missing values in the output variable'
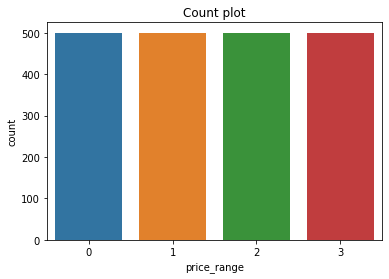
Luckily, there are no missing values! Also, we can see as well that the classes are evenly distributed!
It is great for us! Let me show you the reason…
Suppose the price range is distributed as 90% class 0, 10% class 1 and 0% class 2 and 3. If we built a model that the output is class 0 regardless of the input, we would be right 90% of cases!
C - Now, let’s work with the features as well
I used a great tool to show the CORRELATION between the attributes and output.
A high correlation between the output and attribute is great because based on the attribute, you can certainly predict the output.
However, a high correlation among features is bad, because it reduces the performance of your model. Therefore, it may be useful to filter some of the attributes.
It is the same when you have to do a group homework when 2 classmates have strong opinions. They both want to do well on the homework and get an A (high accuracy on predictions), but they spend too much time discussing it (giving the same information).
IMPORTANT :
The heatmap tool only considers the correlation between two variables or, in other words, 2 dimensional. In fact, the correlation may occur in a multi-dimensional space. Even if in a 2-dimensional space there is a low correlation index, if it is added the third attribute, it may show correlation and decrease the effectiveness of the model!
There are different ways to check and deal with correlation among attributes:
- Variance Inflation Factor (VIF)
- PCA
- Dealing with correlation analyzing 2 by 2 attributes
- Among others
#Let's check the correlation between variables and output
corr = train.corr()
plt.figure(figsize=(15,15))
sns.heatmap(corr,cmap='coolwarm')
<matplotlib.axes._subplots.AxesSubplot at 0x7f962d757310>
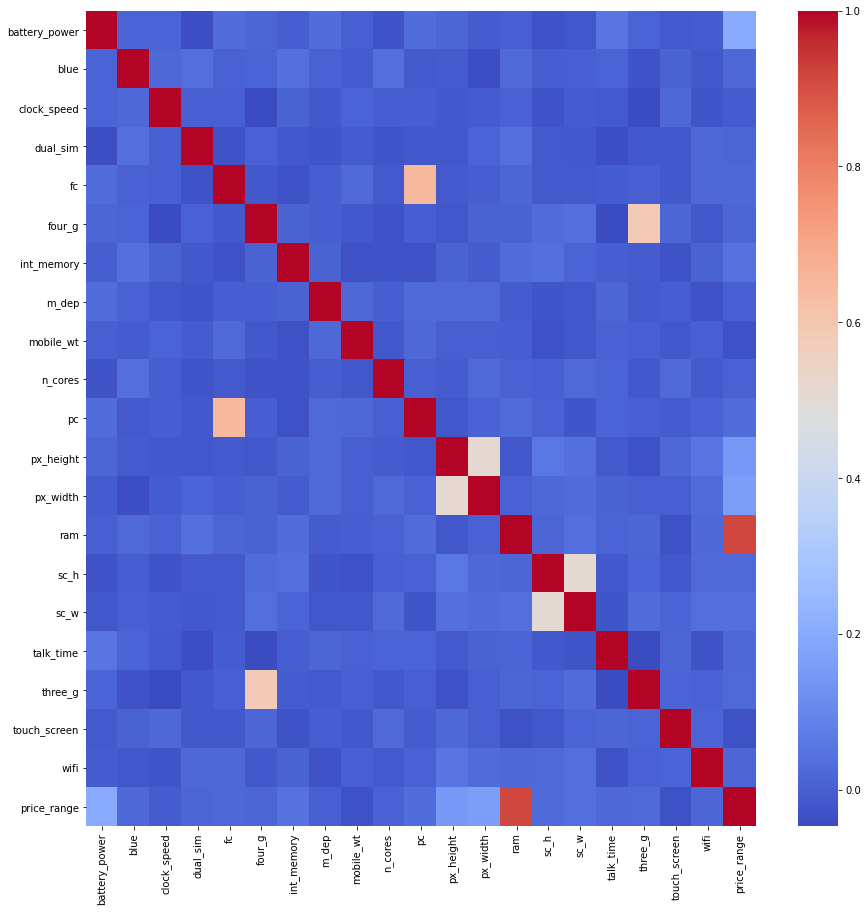
- There are minor correlations between pc/fc and three_g/four_g. However, we are not going to delete any variable. We will keep an eye on these pairs.
- The variable ram has a big role in the price prediction
Missing values - Features
#Missing values train and test set
train_id = train.index.values.shape[0]
test_id = test.index.values.shape[0]
train.drop('price_range',inplace=True,axis=1)
#Collecting ram values
ram = train['ram']
#Train and test data set combined
df = pd.concat([train,test],ignore_index=True)
#Check Missing values
plt.figure(figsize=(15,15))
sns.heatmap(df.isnull(),cbar=False)
<matplotlib.axes._subplots.AxesSubplot at 0x7f962c61f410>

No missing values! Great!
Continuous variables - Checking the probability distribution
The distribution of continuous features plays a big role in the performance of the model in any machine learning problem. The most famous statistical distribution is Normal/Gaussian distribution. Most of all statistical learning models are based on the assumption of normality of data and, in some cases, they may accept deviations from normality.
When working with data, it is important to check the distribution of continuous variables and transform them into Gaussian distribution when possible.
cont = ['battery_power','clock_speed','int_memory','n_cores','m_dep','mobile_wt','pc','px_height','px_width','ram','sc_h','sc_w','talk_time','talk_time']
df_cont = df[cont]
#Distribution plot
row = 7
col = 2
k=0
fig,axes=plt.subplots(row,col,figsize=(15, 15))
for i in range(row):
for j in range(col):
value = cont[k]
sns.distplot(df_cont[value],ax=axes[i][j])
axes[i][j].set_title(value)
k=k+1
plt.tight_layout()
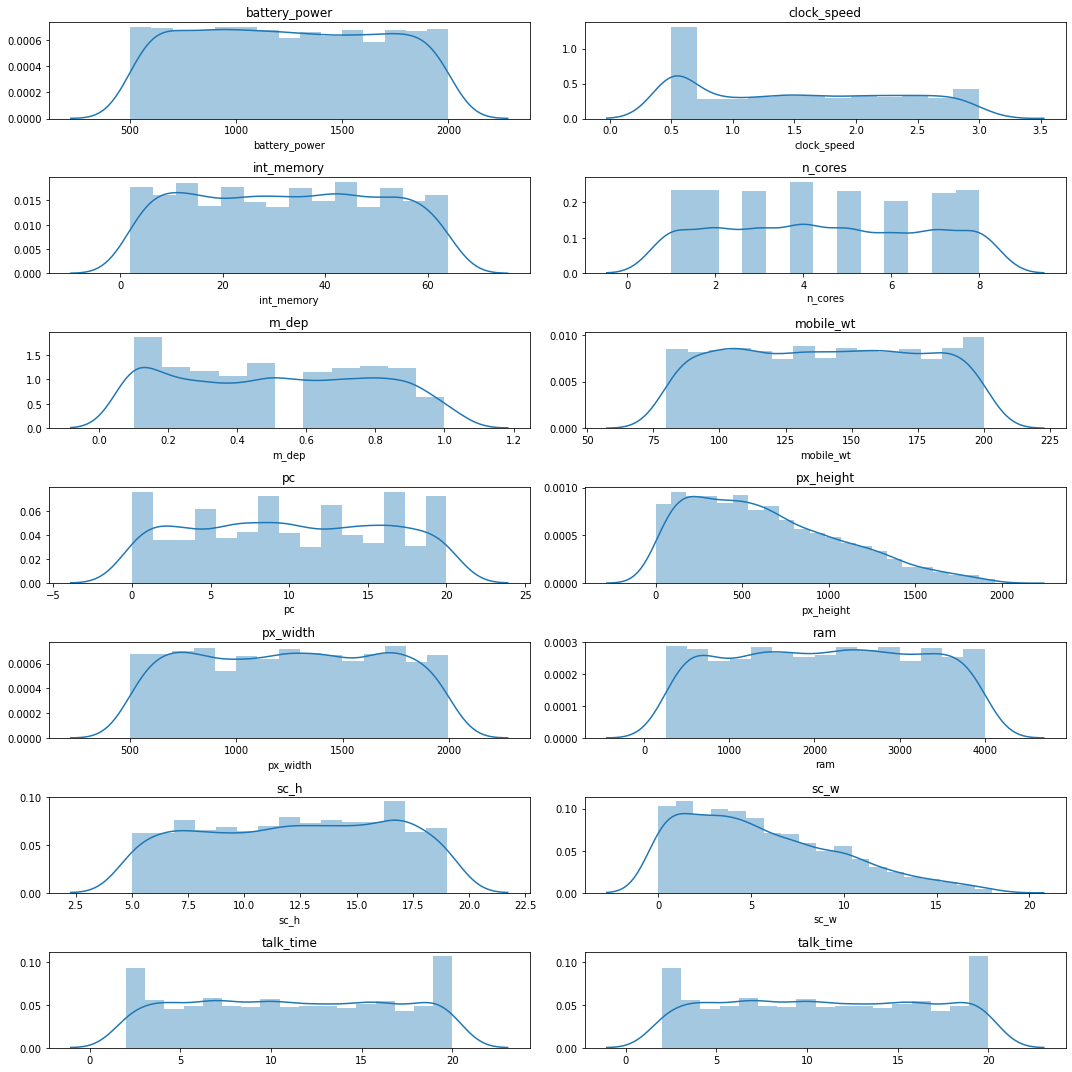
#Checking the distribution of each variable
from scipy.stats import kurtosis, skew
#Quick stats
kurt = kurtosis(df_cont)
skewness = skew(df_cont)
stats = pd.DataFrame([kurt,skewness],columns = cont, index = ['Kurtosis','Skewness'])
stats
| battery_power | clock_speed | int_memory | n_cores | m_dep | mobile_wt | pc | px_height | px_width | ram | sc_h | sc_w | talk_time | talk_time | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kurtosis | -1.206485 | -1.327820 | -1.202377 | -1.221338 | -1.254421 | -1.205739 | -1.194834 | -0.321233 | -1.208986 | -1.191294 | -1.192876 | -0.298492 | -1.207900 | -1.207900 |
| Skewness | 0.033587 | 0.181071 | 0.014648 | 0.043070 | 0.063355 | 0.007305 | 0.012974 | 0.648747 | -0.001558 | -0.011675 | -0.079958 | 0.680002 | 0.011672 | 0.011672 |
Three important parameters to check for normality are the graph, kurtosis and skewness . Here, we can see that no feature presented a normal distribution.
There are several ways to transform the data into normal distribution. However, I failed to find a good way to transform the features that presented a flat distribution.
Therefore, I focused on the “px_height” feature, which presented a right skewed distribution. Also, I realized that Box-Cox transformation does not work well with zero values in the dataset. Then, I used yeo-johnson transformation.
#Transformation - px_height
from sklearn.preprocessing import PowerTransformer
transf =df_cont['px_height'].to_numpy()
lambd = [-2,-1,-0.5,0,1,0.5,1,2]
#for i in lambd:
tr = PowerTransformer(method='yeo-johnson',standardize = True).fit_transform(transf.reshape(-1,1))
sns.distplot(tr)
kurt = kurtosis(tr)
skewness = skew(tr)
print('Kurtosis is {} and Skewness is {}'.format(kurt,skewness))
#The stats are still not good, but let's try it. I have tried the log (1+x) but it does not work good as well (Skewed)
Kurtosis is [-0.66141044] and Skewness is [-0.12665389]
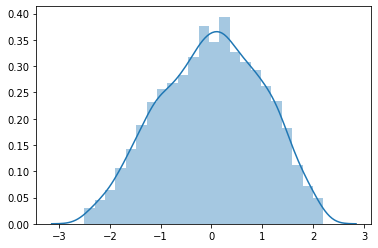
#Updating the new Transformation
df['px_height'] = tr
#Let's settle the train and test dataset
train_set = df.values[:train_id]
test_set = df.values[train_id:]
Multiple classification problem
- We are going to perform two machine learning techiniques: SVM and Logistic Regression.
Plus, we are going to try using only the variable “ram”.
#Importing libraries
from sklearn.preprocessing import RobustScaler,StandardScaler
from sklearn.model_selection import cross_val_score, train_test_split, StratifiedKFold
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier,OneVsOneClassifier
from sklearn.linear_model import LogisticRegression
The two selected models are designed to deal with binary classification problems. However, there are several approaches that manage this situation.
They are: One-vs-Rest (OvR) and One-vs-One (OvO).
It is not my goal here to explain about these methods, but basically they categorize each class by comparing each one of them and each other (one vs one) or other attributes together (one vs rest).
Metrics
Based on a classification problem, there are many metrics to measure the success of the model.
Here, we are going to use the AUC-ROC .
Define a cross validation strategy
We use the cross_val_score function of Sklearn. However this function has not a shuffle attribut, we add then one line of code, in order to shuffle the dataset prior to cross-validation
#Validation function
n_folds = 10
def auc_cv(model):
kf = StratifiedKFold(n_folds, shuffle=True, random_state=100).get_n_splits(train)
auc= cross_val_score(model, train, y_train, scoring="roc_auc_ovr", cv = kf,n_jobs=-1)
return(np.mean(auc))
OBS.: I am using One-vs-Rest.
Training
Support Vector Machine
#Implementing SVC
###Multi class problem
#Train data
train = train_set
#Model
svc = SVC(C=1,kernel='rbf',random_state=43,probability=True)
#Score
score = auc_cv(svc)
print('SVC score = {} based on AUC-ROC'.format(round(score,3)))
SVC score = 0.989 based on AUC-ROC
As we can see, SVM performed pretty well when compared to Logistic Regression. The data presents a non-linear distribution and it is hard for the logistic regression model to perform well. Therefore, based on hyperplanes, SVM achieved a greater metric.
Logistic Regression
#Implementing Logistic Regression
#Train data
#train = ram.reshape(-1,1)
train=train_set
#Model
lreg1 = LogisticRegression(penalty='l2',C=1,class_weight='balanced',random_state=54,multi_class='ovr')
#Score
score = auc_cv(lreg1)
print('Logistic Regression score = {} based on AUC-ROC'.format(round(score,3)))
Logistic Regression score = 0.875 based on AUC-ROC
Logistic Regression with regularization
#Implementing Logistic Regression
from sklearn.linear_model import LogisticRegression
#Train data
train=train_set
#Model
lreg2 = LogisticRegression(penalty='l2',C=0.1,class_weight='balanced',random_state=54,multi_class='ovr')
#Score
score = auc_cv(lreg2)
print('Logistic Regression score = {} based on AUC-ROC'.format(round(score,3)))
Logistic Regression score = 0.876 based on AUC-ROC
Logistic Regression - Feature Engineering
#Implementing Logistic Regression - ONLY WITH RAM
from sklearn.linear_model import LogisticRegression
#Train data
train = ram.values.reshape(-1,1)
#Model
lreg3 = LogisticRegression(penalty='l2',C=1,class_weight='balanced',random_state=54,multi_class='ovr')
#Score
score = auc_cv(lreg3)
print('Logistic Regression score = {} based on AUC-ROC'.format(round(score,3)))
Logistic Regression score = 0.906 based on AUC-ROC
Here, I implemented logistic regression in three different ways to see the importance of regularization and feature engineering.
Regularization is important to reduce the overfitting of your model. Here, it presented a slight improvement in the performance.
However, the greatest improvement was with feature engineering. Feature Engineering is the selection of key features to use in the model instead of using all of them. If all input variables are used, the model may perform poorly since the effects and information of each of them are mixed with each other. Therefore, using only the feature “ram”, we can see an increase in the AUC-ROC metric, which means a greater performance!
Testing
Usually, these kaggle datasets provide a leaderboard, which ranks the performance of your model on test datasets. However, I could not find any board to upload my best model and check its performance. Therefore, I am going to show only the distribution of the predict outputs using the model with the highest metric.
#Training SVM
## Train data
train = train_set
#fit
svc_model = svc.fit(train_set,y_train)
#predict
pred = svc_model.predict(test_set)
#Creating a dataframe
prediction = pd.DataFrame(pred,columns = ['predict'])
#Count plot
sns.countplot(x='predict',data=prediction)
plt.title('Count plot')
Text(0.5, 1.0, 'Count plot')
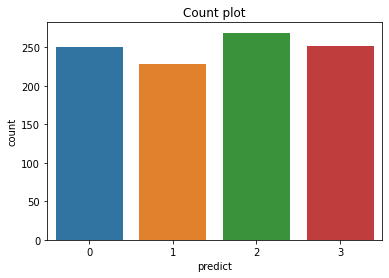
Conclusion
As we can see, the best performance was achieved using SVM as classifier. The data is presented in a non-linear way that lowers the performance of logistic regression. However, there are several ways to increase the performance of the model - feature engineering and regularization.
When testing the model, we noticed that the mobile selling price has a higher chance to be classified as “high cost” based on the dataset.