This project is a little different from the others since I used mainly the Minitab as statistical software. Here, EDA is not extensively discussed. On the other hand, statistical hypotheses and tests are detailed.
To begin with, the goal of this study is trying to confirm if global warming exists and to create critical thinking about the temperature tendency. I was motivated to work on this after seeing the popularity increase of weird theories like Earth being flat.
The dataset is a compilation of several global temperature reports from 1900 to 2015 consolidated by a third-party organization extracted from Kaggle.
Assumptions:
- Confidence level = 95%
Simple Linear Regression
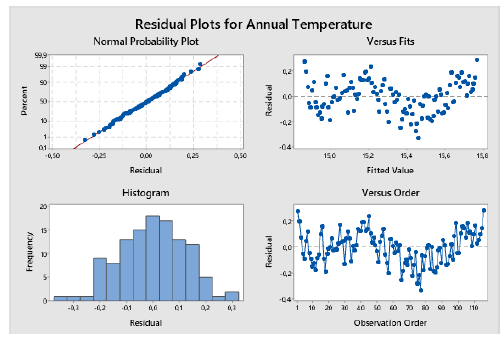
The goal is to evaluate the regression coefficients and check if the global temperature shows an increasing tendency, statistically. The linear regression follows three assumptions that must be attained by performing a residual analysis and they are: normality of the error, homoscedasticity, and independence of the errors.
Graphically, the regression seems to be a great method to adjust the data (R2 = 81.8%). However, residual analysis shows a different reality.
The reason for the violation may be the autocorrelation of the data itself. The annual global temperature is specified as a Time Series, which is defined as a series that intrinsically possesses autocorrelation through time. Then, alternative statistical models must be used.
## Autocorrelation and Time Series Analysis
Time series data is well known by its autocorrelation along the time axis (x-axis), which violates certain assumptions of previous analysis. Here, ARIMA is selected to analyze time series data. ARIMA is the autoregressive integrated moving average model that is based upon the autocorrelation of the values and their random error. Basically, it considers the same assumptions as of the previous linear regression plus the stationarity of the data.
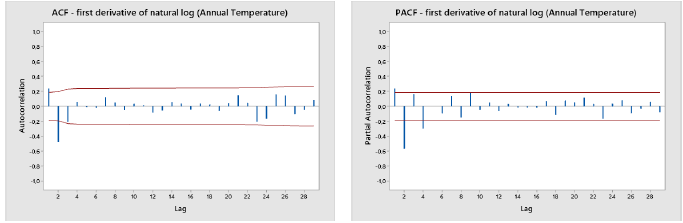
In the first figure, the dataset presents a clear increasing tendency that includes changes in the average through time (non-stationarity). Therefore, there is evidence of the non-stationarity of the dataset. Now, a data transformation is needed and the differentiation method is chosen - the first derivative of the data.
To find the best model, the ACF and PACF correlograms are used.
There are more information about ACF and PACF correlograms on the final report. You can find it on my Git.
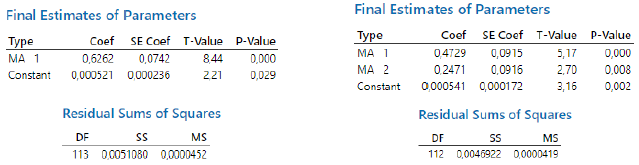
It suggests the two ARIMA models: ARIMA(0,1,1) and ARIMA(0,1,2). On the other hand, in Fig.3 (a), only two correlations are significant (lag 1 and 2) and, after lag 2, it decays exponentially.
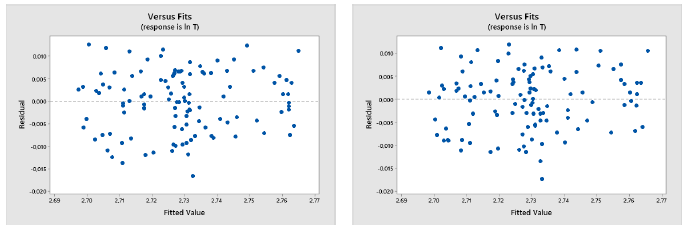
The ARIMA(0,1,2) shows better accuracy in regards to residual sums of squares. Also, when the residuals plots are compared, the ARIMA(0,1,1) residuals show a small dependency on the residuals, which violates the regression assumptions. Therefore, we have enough evidence to use ARIMA (0,1,2) as a model to predict the temperatures through time.
## Conclusions
After all, there is evidence to confirm the increasing tendency of global annual temperature within the periods considered in this work. Considering global warming is associated with the increase in global temperature, we have evidence that global warming exists.
This project suggests as next steps a deeper study on the ARIMA(0,1,2) to forecast future global temperature.
The detailed report with references can be found on my Git.