Hey guys,
From my experience, I can tell that almost everyone has already received a suspicious call asking for confidential information or clicked on a link that could steal important information. In this kind of situation, the person is trying to use your information to access your credit card. It is just one example of many frauds that may happen.
The goal of this study is to develop a Fraud Detection algorithm using several machine learning techniques.
Dataset : I used the Kaggle dataset - Credit Card Fraud Detection The datasets contains transactions made by credit cards in September 2013 by European cardholders, as mentioned in Kaggle description.
Key Takeaways:
- Skewed dataset: How to deal with it.
- Principal Component Analysis.
- Application of Multivariate Gaussian distribution and other machine learning methods.
Update - August 03rd
Additionally to the methods mentioned below on how to deal with the skewed dataset, according to Leevy et al., there are other essential points to take into account.
Imbalance dataset makes difficult for a statistical learning model to discriminate the minority class from the majority one. Then, the following methods are used:
- Data sampling: Random Over-sampling (ROS), Random Under-sampling, and SMOTE.
- Algorithm: Random forest, Neural Networks.
Data Sampling
Here, my goal is not to explain these procedures in details, but all these alternatives are based on the creation of a dataset that would have a balanced distribution between classes by randomly removing samples from majority classes (RUS), duplicating samples from minority classes (ROS) or creating new samples from the similarity between samples on the minority class (SMOTE).
ROS and RUS do not add any information to the model by duplicating nor removing samples. In fact, they can lose information or produce overfitting by the learning models. Considering SMOTE, it usually performs better than the previous methods by attending the mentioned problems.
Here, I am going to use SMOTE and RUS together.
Algorithm
There are a huge amount of alternative statistical learning models to treat an imbalanced dataset. They differ by cost functions, feature selection, hybrid, or ensemble algorithms, among others.
Here, I am going to use Random Forest to check its effectiveness on an imbalanced dataset.
Reference: Leevy, J.; Khoshgoftaar, T.M.; Bauder, R.A.; Seliya, N.;“A survey on addressing the high‑class imbalance in big data”, 2018, Journal of Big Data.
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score
%matplotlib inline
#Importing dataset
df=pd.read_csv('../data/creditcard.csv')
Introduction
The dataset contains numerical values after PCA transformation. The original data could not be shared due to confidentiality issues. Additionally, two features are provided: Time and Amount.
The output is a categoric variable that contains two values - 0 as no fraud and 1 as a fraud.
There are 30 features: Time, Amount and 28 numerical vectors after PCA transformation.
#Let's split the data into three segments: Output, components and other variables
V=[]
for i in range(1,29):
V.append('V'+str(i))
components = df[V]
output = df['Class']
other_var=df[['Time','Amount']]
df.head(10)
Output - Class
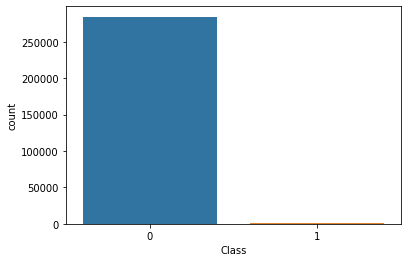
We begin analyzing the output variable - Class
As we can see, the data is skewed with only 0.17% of Class 1.
There are several ways to deal with skewed data. Here, we use:
-
Metric - ROC AUC score. Accuracy is not used here since it would give inaccurate results.
-
Data collection - Even though it was not applied in this study, I added data collection because, if feasible, it is a good option. Data collection was not performed here since all numerical values are PCA transformations already and the original data was not given.
-
Training/Dev/Test set: Caution must be taken when splitting the dataset to proper statistical model training.
Fortunately, there are no missing values as well.
#Output
sns.countplot(x='Class',data=df)
#Data is skewed
zero_prop = round(output.value_counts()[0]/output.count()*100,4)
one_prop = round(100-zero_prop,4)
print('Class 0 is {} % of the data set and Class 1 is {} %.'.format(zero_prop,one_prop))
print('Data is skewed.')
Class 0 is 99.8273 % of the data set and Class 1 is 0.1727 %.
Data is skewed.
#Missing values
print('The output variable has {} % of missing values.'.format(output.isnull().sum()/len(output)*100))
The output variable has 0.0 % of missing values.
Feature Analysis - PCA
The principal component analysis is a statistical method to high dimensional data onto a lower-dimensional space by maximizing the variance of each dimension.
In machine learning, it is commonly used as a way to prevent overfitting, but it is not recommended to be the first solution since it throws away information from the data - regularization may be the first option.
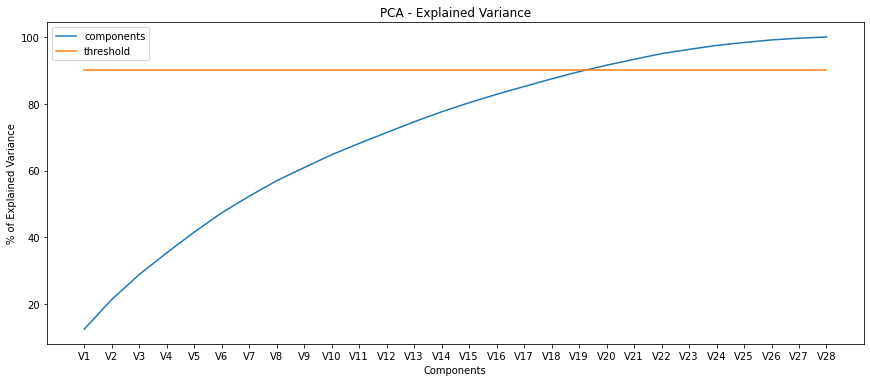
In this study, the numerical values after PCA transformation were already given. Here, I analyze the number of components we may consider following a threshold. The threshold is based on the explained variance and set equals 90%.
#Components of PCA
### Explained Variance
var_vec = components.var(axis=0)
total_var = var_vec.sum()
exp_var = var_vec/total_var
exp_var_cum=np.cumsum(np.round(exp_var, decimals=4)*100)
thresh = np.ones(len(exp_var_cum))*90
#PCA plot
plt.subplots(figsize=(12,5))
plt.plot(exp_var_cum,label='components')
plt.plot(range(len(exp_var_cum)),thresh,label='threshold')
plt.tight_layout()
plt.ylabel('% of Explained Variance')
plt.xlabel('Components')
plt.title('PCA - Explained Variance')
plt.legend()
#Conclusion
#We can see that using until 20 components can explain at least 90% of the total variance.
#OBS.: Total variance is equal to the sum of the variance of all components.
<matplotlib.legend.Legend at 0x7f510175cf50>
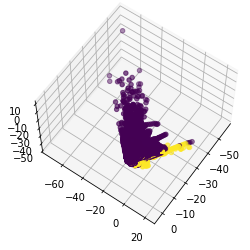
Output and PCA: Plot
Even though we selected the first 20 components. Here, we are going to use V1, V2, and V3 to plot them with the output. Using more than 3 components makes it difficult to visualize their relation with the output.
#PCA and output plot
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(components['V1'],components['V2'],components['V3'],c=output)
ax.view_init(60, 35)
Features - Missing Values
Fortunately, there is no missing values.
#Missing values - PCA Components
print('The components have {} % of missing values.'.format(components.isnull().sum().sum()/len(components)*100))
The components have 0.0 % of missing values.
#Other variables - Time and Amount
print('The other variables have {} % of missing values.'.format(other_var.isnull().sum().sum()/len(other_var)*100))
The other variables have 0.0 % of missing values.
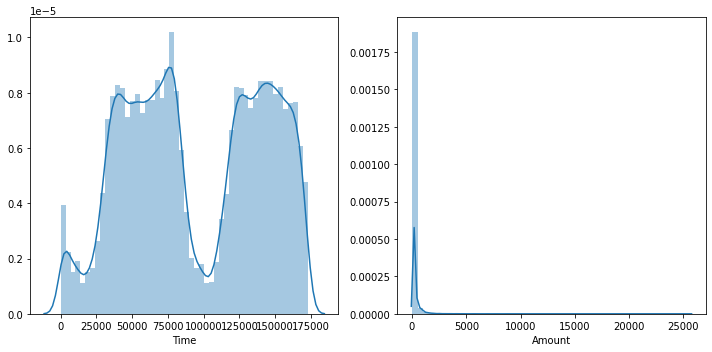
Time and Amount variables: Distribution
It does not make sense to analyze the distribution of numerical since they are results of PCA transformation. Then, I analyze the distribution of Time and Amount variables and perform transformations, if needed.
#Other variables - Plot
fig,axes=plt.subplots(1,2,figsize=(10, 5))
sns.distplot(other_var['Time'],ax=axes[0])
sns.distplot(other_var['Amount'],ax=axes[1])
plt.tight_layout()
#### Data Transformation - Box Cox x+1
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PowerTransformer
t = other_var['Time'].to_numpy()+1
amt = other_var['Amount'].to_numpy()+1
#Time
power = PowerTransformer(method='box-cox',standardize=True)
power.fit(t.reshape(-1,1))
t_std = power.transform(t.reshape(-1,1))
#Amount
power.fit(amt.reshape(-1,1))
amt_std = power.transform(amt.reshape(-1,1))
#Plot
fig,axes=plt.subplots(1,2,figsize=(10, 5))
sns.distplot(t_std,ax=axes[0])
axes[0].set_xlabel('Time')
sns.distplot(amt_std,ax=axes[1])
axes[1].set_xlabel('Amount')
plt.tight_layout()
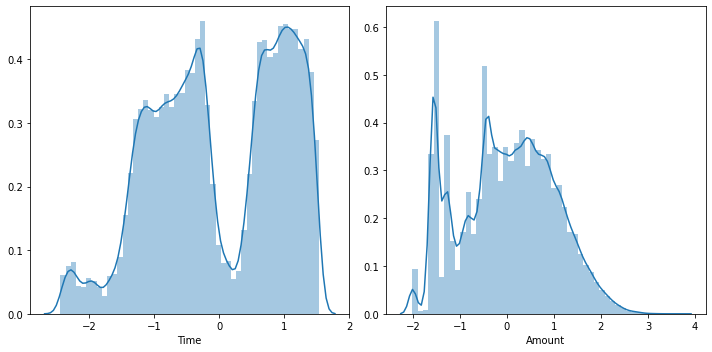
#Updating new variables
df['Time'] = t_std
df['Amount'] = amt_std
Model selection
Note: Data is skewed. We we have to be careful with several aspects: metrics, model selection,train/dev/test set and consider if data generation is an option.
Metrics to be used - ROC AUC
I tried four different statistical models:
- Multivariate Gaussian Distribution
- Logistic Regression
- Support Vector Machine
- Random Forest
### Splitting dataset
from sklearn.model_selection import train_test_split
###### Class 0
class_0 = df[df['Class']==0].drop(['Class'],axis=1)
out_0 = output[output==0]
########## Without Class and Amount
[zero_train,zero_temp,y_zero_train,y_zero_temp] = train_test_split(class_0,out_0,test_size=0.2,random_state=53,shuffle=True)
[zero_dev,zero_test,y_zero_dev,y_zero_test] = train_test_split(zero_temp,y_zero_temp,test_size=0.5,random_state=50,shuffle=True)
##### Class 1
class_1 = df[df['Class']==1].drop(['Class'],axis=1)
out_1 = output[output==1]
########## Without Class and Amount
[one_train,one_temp,y_one_train,y_one_temp] = train_test_split(class_1,out_1,test_size=0.2,random_state=53,shuffle=True)
[one_dev,one_test,y_one_dev,y_one_test] = train_test_split(one_temp,y_one_temp,test_size=0.5,random_state=50,shuffle=True)
##### Consolidating(full - all variables, w/o full - no time and amount var)
## Train
x_train_full = pd.concat([zero_train, one_train], axis=0)
x_train = x_train_full.drop(['Time','Amount'],axis=1)
y_train = pd.concat([y_zero_train, y_one_train], axis=0)
#Dev
x_dev_full = pd.concat([zero_dev, one_dev], axis=0)
x_dev = x_dev_full.drop(['Time','Amount'],axis=1)
y_dev = pd.concat([y_zero_dev, y_one_dev], axis=0)
#Test
x_test_full = pd.concat([zero_test, one_test], axis=0)
x_test = x_test_full.drop(['Time','Amount'],axis=1)
y_test = pd.concat([y_zero_test, y_one_test], axis=0)
Multivariate Gaussian Distribution
Here, we assume that the dataset follows a normal distribution. Then, we calculate the probability of each example and based on a threshold, we classify it.
### Model - Anomaly Detection (Suppose all variable follow a normal distribution)
from scipy.stats import multivariate_normal
cov = np.cov(x_train,rowvar = False)
mu = np.mean(x_train)
prob_train = multivariate_normal.pdf(x_train,mean=mu,cov=cov)
#Choosing the best threshold
prob_dev = multivariate_normal.pdf(x_dev,mean=mu,cov=cov)
### Dev set - Choosing the best threshold
def select_eps(y_dev,prob_dev):
bestEps = 0;
bestroc = 0;
roc= 0;
stepsize = (max(prob_dev)-min(prob_dev))/1000
for eps in np.arange(min(prob_dev),max(prob_dev)+stepsize,stepsize):
pred = prob_dev < eps
roc = roc_auc_score(y_dev,pred)
if roc > bestroc:
bestroc = roc
bestEps = eps
return bestEps,bestroc
# The best eps
[eps,roc] = select_eps(y_dev,prob_dev)
#Test set Score
prob_test = multivariate_normal.pdf(x_test,mean=mu,cov=cov)
pred = prob_test < eps
roc_test = roc_auc_score(y_test,pred)
print('Based on ROC score as metric, assuming the dataset follows a multivariate gaussian distribution, the score is {}%'.format(round(roc_test*100,4)))
print(' ')
Based on ROC score as metric, assuming the dataset follows a multivariate gaussian distribution, the score is 74.6126%
### Splitting dataset
######
x = df.drop(['Class'],axis=1)
y = output
[x_train,x_test,y_train,y_test] = train_test_split(x,y,test_size=0.2,random_state=53,shuffle=True)
#### Cross Validation model
from sklearn.model_selection import RepeatedStratifiedKFold
cv = RepeatedStratifiedKFold(n_splits=10,n_repeats=3,random_state=42)
Logistic Regression - Cross Validation
Here, I try two different logistic regression models:
- Without regularization - All components
- Without regularization - 20 components
- After SMOTE and RUS - All components
Cross Validation - Both Logistic Regression and Random Forest
I used the Repeated Stratified KFold as cross validation method. It runs the models “n” times and keeps the original dataset distribution on each created fold (K = 10 folds).
##### Data set with the first 20 components
## Train
x_train_20 = x_train.drop(['V21','V22','V23','V24','V25','V26','V27','V28'],axis=1)
#Test
x_test_20 = x_test.drop(['V21','V22','V23','V24','V25','V26','V27','V28'],axis=1)
# Logistic Regression
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
#First choice - No regularization
lreg = LogisticRegression(penalty='l2',C=1,fit_intercept = True, max_iter=500,random_state=46)
scores1 = cross_val_score(lreg,x_train,y_train,scoring='roc_auc',cv=cv,n_jobs=-1)
#Second choice - No regularization, but with 20 components
scores2 = cross_val_score(lreg,x_train_20,y_train,scoring='roc_auc',cv=cv,n_jobs=-1)
print('Logistic regression - All components : {} and 20 components: {}'.format(round(np.mean(scores1),4),round(np.mean(scores2),4)))
print(' ')
Logistic regression - All components : 0.9731 and 20 components: 0.9754
### SMOTE and RUS
from imblearn.pipeline import Pipeline
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import RandomUnderSampler
over = SMOTE(sampling_strategy = 0.1)
under = RandomUnderSampler(sampling_strategy = 0.5)
steps = [('over',over),('under',under),('model',lreg)]
pipeline1 = Pipeline(steps=steps)
scores = cross_val_score(pipeline,x_train_20,y_train,cv=cv,scoring='roc_auc',n_jobs=-1)
print('After preprocessing with SMOTE and RUS, Logistic regression performance is {}'.format(round(np.mean(scores),4)))
After preprocessing with SMOTE and RUS, Logistic regression performance is 0.9755
Random Forest - Cross Validation
Random Forest is one of several methods recognized by achieving good performance on an imbalanced dataset. Therefore, I apply it in this study.
At first, I search for the best number of trees. I considered that using 20 PCA components, Time and Amount features would achieve greater metrics based on the previous tests on logistic regression. ( This is a dangerous assumption since this test should have been done using the random forest as well. )
After finding the best forest, we are going to compare it with the Logistic Regression.
# Random Forest - Finding the best number of trees
from sklearn.ensemble import RandomForestClassifier
cv1 = RepeatedStratifiedKFold(n_splits=10,n_repeats=1,random_state=42)
est = [10,25,100]
auc_forest = []
for value in est:
forest = RandomForestClassifier(n_estimators=value,criterion ='gini' , max_features ='sqrt',n_jobs=-1)
scores = cross_val_score(forest,x_train_20,y_train,cv=cv1,scoring='roc_auc',n_jobs=-1)
auc_forest.append(np.mean(scores))
#Plot
plt.plot(est,auc_forest)
plt.xlabel('Number of trees')
plt.ylabel('ROC AUC score')
plt.title('Random Forest - Optimum number of trees')
Text(0.5, 1.0, 'Random Forest - Optimum number of trees')
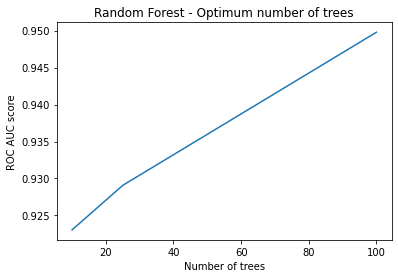
### 1000 trees - Without data sampling
forest = RandomForestClassifier(n_estimators=1000,criterion ='gini' , max_features ='sqrt',n_jobs=-1)
scores_1000 = cross_val_score(forest,x_train_20,y_train,cv=cv,scoring='roc_auc',n_jobs=-1)
np.mean(scores_1000)
0.959761932795856
### Random Forest with data sampling
steps = [('over',over),('under',under),('model',forest)]
pipeline = Pipeline(steps=steps)
scores = cross_val_score(pipeline,x_train_20,y_train,cv=cv,scoring='roc_auc',n_jobs=-1)
print('After preprocessing with SMOTE and RUS, Random Forest performance is {}'.format(round(np.mean(scores),4)))
After preprocessing with SMOTE and RUS, Random Forest performance is 0.986
Random forest performed better than Logistic Regression. Therefore, it is the best model for this study.
Test set
Then, let’s see how it performs on test set!
### Random Forest with data sampling
forest = RandomForestClassifier(n_estimators=1000,criterion ='gini' , max_features ='sqrt',n_jobs=-1)
steps = [('over',over),('under',under),('model',forest)]
pipeline = Pipeline(steps=steps)
pipeline.fit(x_train_20,y_train)
pred = forest.predict(x_test_20)
final_score = roc_auc_score(y_test,pred)
print('Random forest - ROC AUC: {}'.format(round(final_score,4)))
Random forest - ROC AUC: 0.9402
Conclusion
It is amazing to see this usage of data to prevent fraudulent transactions or any other application.
At first glance, the data could look like just as “just numbers”. However, they were used for a greater good. Extracting information from data and seeing a trend behind numbers is what I find exciting about data science.
Here, the random forest model is chosen as the best model to help the detection of fraudulent transactions. Using data sampling techniques such as SMOTE and feature selection improved the model. The final ROC AUC score on the test set was 94.02% .